Research Projects
My current research interests are computational and approximate inference with applications in machine learning, signal processing and system identification. Examples include Monte Carlo and Variational Bayesian methods for inference and learning in Probabilistic Graphical Models (PGM).
- Variational Inference
- Nested Sequential Monte Carlo
- Sequential Monte Carlo Methods for Graphical Models
Google scholar profile: C. A. Naesseth
Variational Inference
We synthesize variational with Monte Carlo methods to leverage the benefits of both.
- C. A. Naesseth, S. W. Linderman, R. Ranganath, and D. M. Blei, Varational Sequential Monte Carlo. arXiv, arXiv:1705.11140, 2017. C*
- C. A. Naesseth, F. J. R. Ruiz, S. W. Linderman, and D. M. Blei, Reparameterization Gradients through Acceptance-Rejection Sampling Algorithms. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, Fort Lauderdale, USA, April 2017. C6
Nested Sequential Monte Carlo Methods
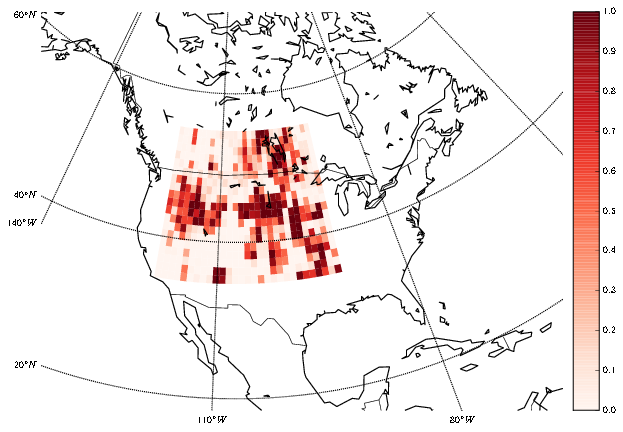
Nested sequential Monte Carlo (NSMC) is a methodology to sample from sequences of probability distributions, even where the random variables are high-dimensional. NSMC generalises the SMC framework by requiring only approximate, so called properly weighted, samples from the SMC proposal distribution, while still resulting in a correct SMC algorithm. This enables efficient particle filtering in high-dimensional, complex, statistical models.
We illustrate the merits by extensive evaluation on both synthetic as well as real data. Specifically in the real data example we consider a climatological model for drought prediction, with a 1056-dimensional state space. For more information see our ICML 2015 paper.
- C. A. Naesseth, F. Lindsten and Thomas B. Schön, Nested Sequential Monte Carlo Methods. Proceedings of the 32nd International Conference on Machine Learning, Lille, France, July 2015. C3
Sequential Monte Carlo Methods for Graphical Models
Probabilistic graphical models is a fairly general and intuitive framework for representing and make use of underlying structure in probability distributions. Applications can be found in such diverse areas as computer vision, biology, machine learning, information theory and many, many more. What they all have in common is statistical inference in general is intractable and approximate methods are needed. We have developed several sequential Monte Carlo (SMC)-based methods for coping with this problem. SMC is a powerful framework and alternative (or complement) to classical Monte Carlo methods such as Markov chain Monte Carlo.
Sequential Monte Carlo
We introduce a first basic way of adapting the SMC algorithm to PGMs, with extensions to particle MCMC methods, in our NIPS 2014 paper.
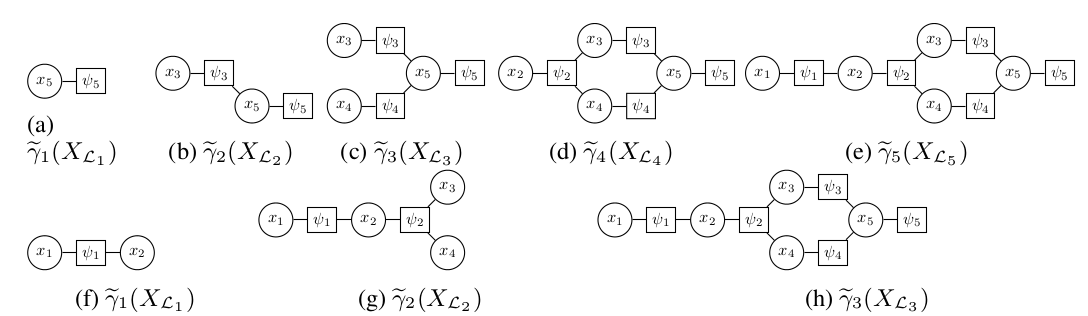
- C. A. Naesseth, F. Lindsten and T. B. Schön, Sequential Monte Carlo for Graphical Models. Advances in Neural Information Processing Systems (NIPS) 27, Montreal, Canada, December 2014. C2
We have also published some preliminary results and an interesting application in information theory:
- C. A. Naesseth, F. Lindsten and T. B. Schön, Capacity estimation of two-dimensional channels using Sequential Monte Carlo. Proceedings of the 2014 IEEE Information Theory Workshop (ITW), Hobart, Australia, November 2014. C1
Divide-and-Conquer with Sequential Monte Carlo
We are currently working on divide-and-conquer with sequential Monte Carlo (D&C-SMC), a completely new class of SMC algorithms inspired by inference in PGMs that runs naturally on tree-structured decompositions of PGMs. We introduce the algorithm and potential extensions in our working paper.
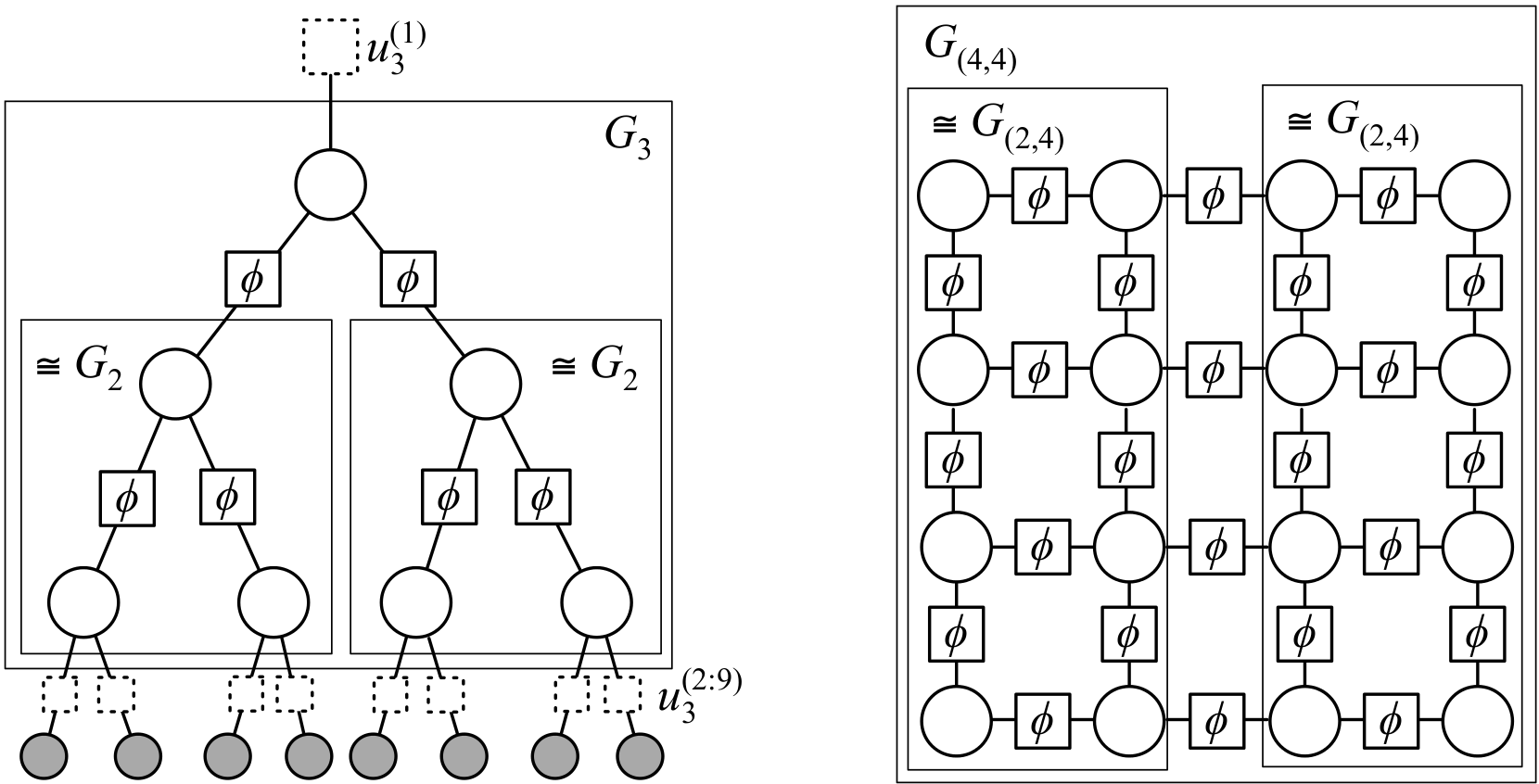
- F. Lindsten, A. M. Johansen, C. A. Naesseth, Bonnie Kirkpatrick, Thomas B. Schön, John Aston and Alexandre Bouchard-Côté, Divide-and-Conquer with Sequential Monte Carlo. arXiv.org, arXiv:1406.4993. J1*
For more information about my work please see the publications, presentations and source code pages.

PhD Student in Automatic Control
(Swedish: Doktorand i reglerteknik)
- Phone:
- +46 13 281087
- E-mail:
- christian.a.naesseth_at_liu.se
- Address:
- Dept. of Electrical Engineering
- Linköping University
- SE-581 83 Linköping
- Sweden
- Visiting Address:
- Campus Valla
- Building B
- Room 2A:522 (in the A corridor on the ground floor between entrance 25 and 27)
Page responsible: Christian Andersson Naesseth
Last updated: 2017-08-17
 LiU startsida
LiU startsida
